Representation of Cartesian product of sets

I. Arrow diagram:

We may represent the Cartesian product of the sets by an arrow diagram.

Ex1:

If A = {3, 4, 5} and B = {6, 8, 10}, then represent A × B in an arrow diagram.

Sol:

Given, A = {3, 4, 5} and B = {6, 8, 10}.
Here, n(A) = 3 and n(B) = 3.

A × B = {3, 4, 5} × {6, 8, 10}

Now the arrow diagram for A × B is as follows:

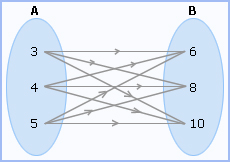
From the above diagram, we can conclude the ordered pairs as:

A × B = {(3, 6), (3, 8), (3, 10), (4, 6), (4, 8), (4, 10), (5, 6), (5, 8), (5, 10)}

n(A × B) = 9

Ex2:

If A = {p, q} and B = {k}, then represent A × B in an arrow diagram?

Sol:

Given, A = {p, q} and B = {k}.

n(A) = 2, n(B) = 1.

n(A × B) = 2 × 1 = 2

Now the arrow diagram for A × B is as follows:

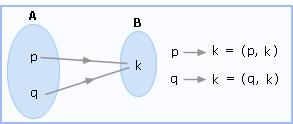From the above diagram, we can conclude the set of ordered pairs as:

A × B = {p, q} × {k} = {(p, k), (q, k)}

II. Tree diagram:

We may represent the Cartesian product of the sets by a tree diagram.

Ex1:

Let P = {a, b, c} and Q = {m, n} be two sets. Represent P × Q in a tree diagram.

Sol:

Given, P = {a, b, c} and Q = {m, n}.

n(P) = 3, n(Q) = 2.

n(P × Q) = 3 × 2 = 6

Now the tree diagram for P × Q is as follows:

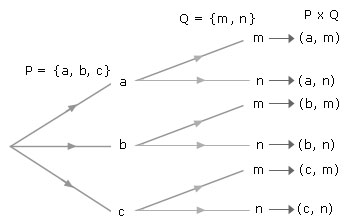
From the above diagram:

P × Q = {a, b, c} × {m, n}

P × Q = {(a, m), (b, m), (c, m), (a, n), (b, n), (c, n)}.

Ex2:

From the following tree diagram, find A × B.

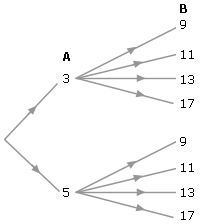
Sol:

From above diagram, we can conclude that

A = {3, 5} and B = {9, 11, 13, 17}

n(A) = 2 and n(B) = 4

n(A × B) = 2 × 4 = 8

A × B = {3, 5} × {9, 11, 13, 17}

A × B = {(3, 9), (3, 11), (3, 13), (3, 17), (5,9), (5, 11), (5, 13), (5, 17)}

III. Graphical representation of Cartesian product:

The Cartesian product can be represented in a graphical form.

Example:

If A = {1, 2, 3, 4} and B = {1, 2, 3}, then represent A × B in a graph.

Procedure:

Draw two lines one horizontal line and vertical line which are perpendicular to each other.

Represent the first set elements 1, 2, 3, 4 on horizontal line and represent the second set elements 1, 2, 3 on vertical line.

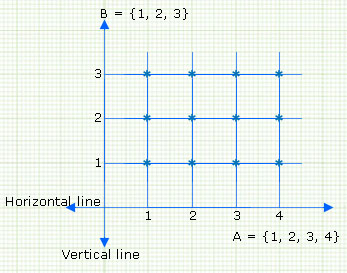
Draw lines 1, 2, 3 which are parallel to the horizontal line.

Similarly draw lines from 1, 2, 3, 4 which are parallel to vertical line.

The intersection of vertical line and horizontal line are represented as '*'.

The '*' represents the ordered pairs of the set A × B.

So, from the graph, the ordered pairs are:

(1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (3, 3), (4, 1), (4, 2), (4, 3)

∴ The set A × B = {(1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (3, 3), (4, 1), (4, 2), (4, 3)}