Why does a helicopter have a small fan in its rear tail, in addition to its main large rotor ?
Helicopter rises vertically because of Newton's third law of motion. The rotors are angled in such a manner that when they start rotating, they push a large volume of air downwards. The air in turn pushes the helicopter upwards.
This is fine; but due to its rotation, the body of the helicopter will start rotating around too. Try hanging a toy of a string from a ceiling fan. Switch on the fan - as the fan rotates, the toy will also start rotating. (Now some of you may have a doubt that why doesn't the fan start rising up! Well the fan is bound tightly with a large hook and bolts to the ceiling. Also the helicopter blades are really long and angled in such a manner that they are able to displace air downwards. Such mechanisms are not present in case of a ceiling fan).
The helicopter body starts rotating because it gets an angular momentum due to the rotation of the blades. Since the blades rotate in the horizontal plane, the angular momentum generated by them L = r x p would be either vertically upwards or downwards. If L is upwards, the helicopter body will rotate in an anti - clockwise fashion and vice versa. To counteract this L, a small fan is placed on the tail of the helicopter. The fan is made to rotate in the vertical plane. Its angular momentum l, will be perpendicular to L. Both these angular moments L and l counteract so that the net angular momentum vector is null.
The small fan is so important to the stability of the helicopter that if it breaks apart, the helicopter will become unstable and will go into a spin.
A tyre is set into circular motion on an axis. You stand on a friction-free rotating platform and hold the tyre. The tyre is rotating in an anti - clockwise direction. You flip the tyre so that now it's rotating in a clockwise direction. Why do you start rotating in the anti clockwise direction tyre when it is flipped?

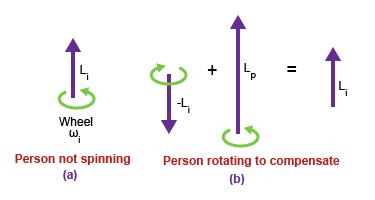
Angular momentum L is a conserved quantity. Let L be the angular momentum of the tyre when it's rotating in the anti-clockwise direction. L is directed upwards. Your angular momentum is zero. The initial angular momentum of you and the tyre together is L.
You now flip the tyre. The tyre's angular momentum is flipped,to -L. To get back the original angular momentum L, you start rotating in an anticlockwise direction so that your angular momentum is 2L.
Why is Earth oblate in shape?
The belief that the shape of our Earth is spherical is not really correct. Earth is slightly flattened at the poles and is bulged at the equator.
The Earth is more like an orange than a football. Why is this so ?
The reason lies in the fact that Earth is rotating on its axis. When a system is undergoing circular motion, extra forces arise in its frame of reference. One such force is the centripetal force. You must have experienced the effect of centripetal force while traveling in a car that is making a turn. You tend to feel a force that is opposite to the direction of turning. Your body's inertia is resisting the effect of the centripetal force.
The angular speed of Earth's rotation is given by ω = 360°/24 hour. The force experienced at different points on the Earth is Mω 2r, where r is the distance of the point from the axis of rotation, and M is the mass at that point.
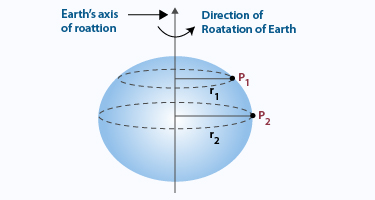
Consider two points P 1 and P 2 on the surface of the Earth. P 1 is close to one of the poles and P 2 is at the equator. Let r 1 be the distance of P 1 from the axis of rotation. Let r 2 be the distance of P 2 from the axis of rotation. It can be seen that r 2 is much greater than r 1 (r 2 >> r 1). Let two identical masses M 1 be situated at P 1 and P 2. Due to Earth's rotation, the force at P 1 will be M 1ω 2r 1, and at P 2 it will be M 1ω 2r 2. Because r 2 >> r 1, M 1ω 2r 2 >> M 1ω 2r 1. This means that the effect of the centripetal force at P 2 is greater than at P 1.
As mentioned before, the inertia of the centripetal force is directed outwards, away from the axis of rotation. Thus the mass at the equator will experience a higher outward force than the mass at the pole. This stretches the mass at the equator. The outward bulge at the equator is because of this reason. The Earth therefore gets its shape more like an oblate orange rather than a spherical football.
It has to be emphasized here that if Earth's composition were very rigid and hard, this deformation would not have been so pronounced. All bodies that rotate will eventually acquire an oblate shape, due to the presence of the inertia to the centripetal force.
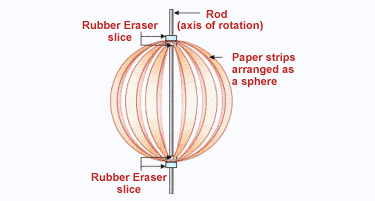
To appreciate how Earth deforms into an oblate shape, do the following experiment. For this you will need :
- A thin rigid rod about 10 inches in length and having a diameter of about 1 mm or 2 mm.
- 8 to 10 paper strips, about 8 inches in length and 2 cm in width.
- 4 paper circles, diameter 3 to 4 cm, with a central hole through which the rod can pass.
- Rubber eraser cut into 4 thin slices.
Take one paper circle. Stick the paper strips on it at equal angular distance or symmetrically. Take the rod. Push one eraser slice in it. Place this paper circle with strips on it into the rod. Then place another paper circle and stick the paper circles together. Place another eraser slice on this. The eraser slices ensure that the paper circles are held on place and don't slip off on the rod.
On the other end of the rod, push the third eraser slice and then another paper circle. Stick the loosely hanging paper strips on this circle. Place the fourth paper circle and stick it. Lastly place the fourth eraser slice.
Slide the eraser slices on the rod so that the paper strips take a spherical shape. Now rotate the rod (axis or rotation) and see how the paper sphere is getting deformed into an oblate shaped object. Instead of paper you can use other materials like plastic sheets, aluminium foils, etc. Change the thickness of the strips, speed of rotation and observe the difference in the shape deformation.
Why do cyclones go anticlockwise in the northern hemisphere and clockwise in the southern hemisphere?
The Earth is rotating on its axis with an angular velocity ω . The rotational motion introduces some "extra" forces which are not explained by the F = ma kind of an equation. These extra forces are also known as fictitious forces. One such force is known as Coriolis force, which was discovered by a French mathematician Gustave-Gaspard Coriolis in 1835.
Coriolis force has the form v x ω, where linear v is the velocity of the object in motion and ω is the angular velocity of Earth's rotation. The Coriolis effect is maximum for an object travelling in the north-south longitude. If you apply the right hand rule for cross vector product of v x ω, you will see that the Coriolis force effects a displacement of the object in motion. The deflection is to the right side in the northern hemisphere and to the left side in the southern hemisphere. The Coriolis effect is especially seen in satellite images of cyclones when large air mass is travelling from high pressure regions to low pressure regions. The cyclones are always anticlockwise in the northern hemisphere and clockwise in the southern hemisphere.
The Coriolis effect is in general seen in many cases. Right banks of rivers in northern hemisphere are always more eroded. Same is true with the erosion of right hand side of a railway track in the northern hemisphere.