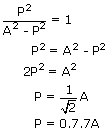A particle of mass 0.5 kg is executing SHM of amplitude 0.03m. When the particle passes through the mean position its kinetic energy is 10 × 10 −3J. Obtain the equation of motion of this particle of the initial phase of oscillation in 45°?
Equation of motion of a particle in simple harmonic motion is
| Given, x | = | ACos(ωt + Φ) |
| Amplitude A | = | 0.3 m |
| Initial phase Φ | = | 45° |
| = | 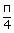 rad rad |
|
| Mass of the particle m | = | 0.5 kg |
| Kinetic energy at the mean position Ek | = | 10 × 10−3J |
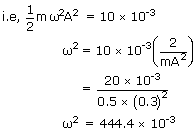
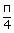 )
)A particle of mass 0.2kg executes a SHM of amplitude 2 cm and period 6 seconds. Find the total mechanical energy at any instant and the kinetic and potential energies when displacement is 1 cm ?
| Mass of the particle m | = | 0.2 kg |
| Amplitude of the motion A | = | 2 cm |
| = | 0.02 m | |
| Time period T | = | 6 sec |
| Angular frequency ω | = | 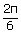 rad/s rad/s |
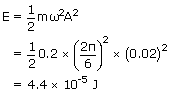
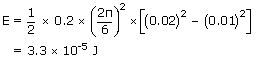
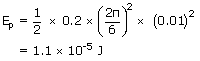
An object of mass 3 kg is attached to a spring with spring constant k = 280N/m and is executing simple harmonic motion when the object is 0.02m from its equilibrium position it is moving with a speed of 0.55m/s. Calculate the amplitude of the motion and maximum velocity attained by the object?
Given,
| Mass of the object m | = | 3 kg |
| Spring constant k | = | 280 N/m |
| Displacement x | = | 0.02m |
| Speed of the object v | = | 0.055m/s |
| Amplitude of motion A | = | ? |
| Maximum Velocity Vmax | = | ? |
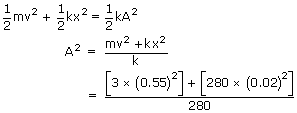
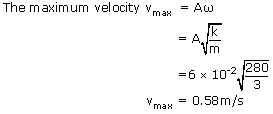
At what displacement from equilibrium is the energy of a simple harmonic oscillator half P.E and half K.E ?
| Total energy E | = | ½ mω2 A2 |
| where A is amplitude | ||
| Let x | = | pm be the displacement where the energy is half P.E and half K.E |
| i.e at x | = | P |
| P.E | = | ½ E |
| K.E | = | ½ E |
| We get two equations, | ||
| ½ mω2P2 | = | ½ [½ mω2A2] and |
| ½ mω2(A2− P2) | = | ½ [½ mω2A2] |