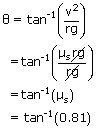The orbit of the moon about the earth, which is nearly circular has a radius of about 384000 km and a period T of 27.3 days. Determine the acceleration of the moon towards the earth.?
| Radius of the orbit r | = | 384000 km |
| ; | = | 3.84 × 108 m |
| Time required for one complete orbit is | ||
| T | = | 27.3 days |
| = | 27.3 × 24 × 3600 | |
| = | 2.36 × 106 seconds. | |
| velocity of the moon moving around the earth | ||
| v | = | 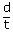
|
| = | 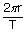
|
|
| = | 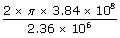
|
|
| = | 10.22 × 102 m/s | |
| The centripetal acceleration of the moon | ||
| a | = | 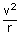
|
| = | 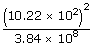
|
|
| = | 27.2 × 10- 4 m/s2 | |
| = | 2.72 × 10- 3 m/s2 |
At what maximum speed can a car safely negotiate a horizontal unbanked turn of radius 60m in dry weather if the coefficient of static friction is 0.95?
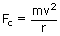
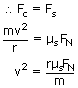
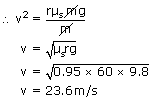
A cyclist goes around a circular track 500m long in 25 seconds. What is the angle that his cycle makes with the vertical to safely cover the circular track ?
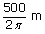
In order to take a safe turn, the cyclist has to bend a little from his vertical position
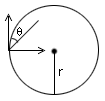
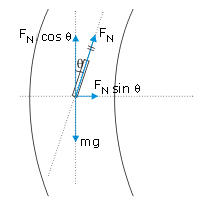
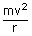
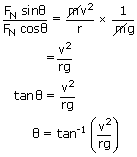
Now we need to find the velocity to determine the safe angle of the cyclist
| Velocity v | = | 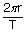
|
| = | 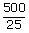
|
|
| ; | = | 20 m/s |
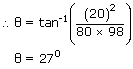
θ = 27° is the angle at which the cyclist should bend to safely cover the track.
Two curves on a highway have the same radii. However, one is banked at angle θ and the other is unbanked. A car can safely travel along the unbanked curve at a maximum speed v0 under conditions when the coefficient of static friction between the tyres and the road is μs = 0.81. The banked curve is frictionless, and the car can negotiate it at the same maximum speed v0. Find the angle θ of the banked curve?
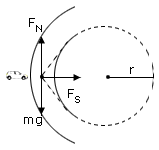
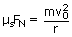
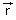
Now, when the car travels along the banked curve, the angle of the curve is given by