Consider an object is in uniform circular motion. The velocity 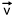has different directions at different places on the circle. At time 't₀' the velocity is tangent to the circle at point 'O' and at a later time 't', the velocity is tangent to the circle at point P. As the object moves from O to P, let the radius trace out an angle θ.

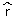
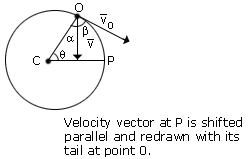
The angle β between the two velocity vectors indicates the change in direction. Since the radii CO and CP are perpendicular to the tangents at the points O and P, θ = β , since α + β = 90° and α + θ = 90°

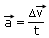
The triangle formed by the velocity vectors 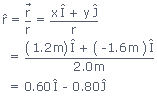is geometrically similar to the triangle COP (as θ = β). In the limit that Δt is very small, the arc length OP is approximately a straight line whose length is the distance vΔt traveled by the object. In this limit ΔCOP is an isosceles triangle.

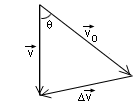
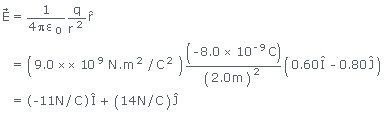
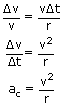
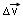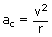which is the magnitude of the centripetal acceleration and its direction along is towards the centre of the circle. The centripetal acceleration is indeed smaller when the radius is larger. In fact, with 'r' in the denominator on the right of , the acceleration approaches zero, when the radius becomes very large. Uniform circular motion along the arc of an infinitely large circle, has zero acceleration, because it is just like motion at a constant speed along a straight line.