Calculate the pressure due to a water–column of height 120 m. (Take g = 10 m s–2 and density of water = 103 kg m –3)?
| Given height of water–column | = | 120 m, g = 10 m s–2 |
| And density of water | = | 103 kg m–3 |
| Pressure | = | h ρ g |
| = | 120 × 103 × 10 | |
| = | 12 × 105 N m–2 |
At what depth below the surface of water will the pressure be equal to the atmospheric pressure ? The atmospheric pressure is 10 N cm –2. Density of water = 103 kg m–3, g = 9.8 m s–2?
| But P | = | 10 N cm–2 |
| = | 10N/(10–2 m)2 | |
| = | 105 N m–2 | |
| Hence h | = | P/ρg |
| = | 105/(103 × 9.8) | |
| = | 10.2 m |
Thus a water column of height 10.2 m exerts a pressure equal to the atmospheric pressure.
A square plate of side 10 m is placed horizontally 2 m below the surface of water. The atmospheric pressure is 1.013 × 105 N m –2. Calculate the total thrust on the plate.(Density of water = 10 3 kg m–3, g = 9.8 m s–2)?
The pressure at a point 2 m below the surface of water = atmospheric pressure = (1.013 × 105 N m2) + pressure due to a column of water of height 2 m.
| Pressure due to 2 m column of water | = | h ρ g |
| = | 2 × 103 × 9.8 | |
| = | 0.196 × 105 N m–2 | |
| ∴ Total pressure | = | (1.013 × 105) + (0.196 × 105) |
| = | 1.209 × 105 N m–2 | |
| Area of the plate | = | 10 × 10 |
| = | 102 m2 | |
| ∴ Total thrust on the plate | = | Pressure × Area |
| = | (1.209 × 105) × 102 | |
| = | 1.209 × 107 N |
When an air bubble rises from the bottom of a lake to the surface, its volume is doubled. Find the depth of the lake. (Atmospheric pressure = 76 cm of Hg, density of Hg = 13.6 g cm–3 and density of water = 1 g cm –3)?
| P1 | = | Atmospheric pressure + pressure due to water column in the lake |
| = | 76 × 13.6 × g + hρg | |
| = | (76 × 13.6 + h × 1) g | |
| Volume of bubble at the bottom, V1 | = | V |
| Volume of bubble at the surface, V2 | = | 2V |
| Pressure at the surface P2 | = | Atmospheric pressure |
| = | 76 cm of Hg | |
| = | 76 × 13.6 × g | |
| From Boyle's law, P1V1 | = | P2V2 |
| (76 × 13.6 + h × 1) g × V | = | 76 × 13.6 × g × 2V |
| or h | = | (2 × 76 × 13.6) – (76 × 13.6) |
| = | 76 × 13.6 | |
| = | 1034 cm | |
| = | 10.34 m |
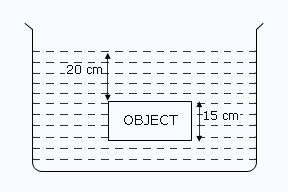
Figure shows a rectangular object immersed in water of density 10 3 kg m–3 Calculate the pressure at the top and bottom of the object, the resultant pressure on the object. Take atmospheric pressure = 10 5 Pa and g = 9.8 N kg–1?
| Atmospheric pressure P0 | = | 105 Pa, |
| g | = | 9.8 N kg–1 |
| Depth of top of the object from water surface h1 | = | 20 cm |
| = | 0.2 m | |
| Depth of bottom of object from water surface h2 | = | 20 + 15 = 35 cm =0.35 m |
| (i) Pressure at the top surface of object P1 | = | Po + h1 ρg |
| = | 105 + (0.20 × 103 × 9.8) | |
| = | 1.0196 × 105 Pa | |
| Pressure at the bottom surface of object P2 | = | Po + h2 ρg |
| = | 105 + (0.35 × 103× 9.8) | |
| = | 1.0343 × 105 Pa | |
| (ii) Resultant pressure on the object | = | P2 – P1 |
| = | (1.0343 × 105) – (1.0196 × 105) | |
| = | 0.0147 × 105 Pa (or 1.47 × 103 Pa) |
A U tube is partially filled with mercury. If water is added in one arm and oil is added in the other arm, calculate ratio of water and oil columns so that the mercury level is the same in the two arms. Given density of water = 103 kg m–3, density of oil = 900 kg m–3?
| i.e., h1ρ1g | = | h2ρ2 g |
| Here h1 | = | height of water column, |
| ρ1 | = | density of water |
| = | 103 kg m–3, | |
| h2 | = | height of oil column, |
| ρ2 | = | density of oil |
| = | 900 kg m–3. | |
| ∴ h1/h2 | = | ρ1/ρ2 |
| = | 900/103 | |
| = | 9/10 |
| (i) Volume of vessel | = | (120 / 100 m) × (80 / 100m) × (200 / 100 m) |
| = | 1.92 m3 | |
| Thrust at the bottom of the vessel | = | Weight of liquid in the vessel. |
| = | Volume × density × g | |
| = | 1.92 × (1.1 × 103) × 9.8 | |
| = | 2.069 × 104 N | |
| (ii) Area of the bottom of vessel | = | (120/100 m) × (80/100m) |
| = | 0.96 m2 | |
| Pressure at the bottom of vessel | = | Thrust/Area |
| = | (2.069 × 104 N)/(0.96 m2) | |
| = | 2.15 × 104 N m–2 | |
| (iii) Pressure at a depth of 5 cm from the free surface | = | hρg |
| = | (5/100) × (1.11 × 103) × 9.8) | |
| = | 539 N m–2 |
(iv) Net force on the metal foil will be zero because the force exerted on each of the two faces of the foil, by the liquid will be equal and opposite.
| (v) Pressure at the bottom of vessel | = | Atmospheric pressure + pressure due to liquid column |
| = | (1.0 × 105) + (0.215 × 105) | |
| = | 1.215 × 105 N m–2 | |
| ∴ Thrust at the bottom | = | Pressure × Area |
| = | (1.215 × 105) × 0.96 | |
| = | 11.664 × 104 N |
In figure, a tube of length 220 cm filled with a liquid of density 0.90 × 103 kg m–3 is placed inclined with the vertical such that the level A of liquid in the tube is at a vertical distance 120 cm from its lowest point C. There is a point B in the tube below the point A at a vertical distance 80 cm. Assuming the atmospheric pressure to be 1.013 × 105 N m –2, calculate the pressure at the points A, B and C. What will be the pressure at the point C when the tube is made vertical ?
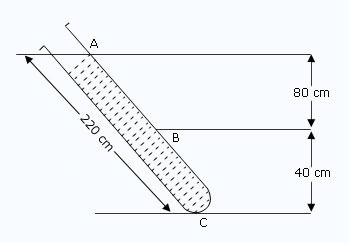
| Pressure at the point A | = | Atmospheric pressure |
| = | 1.013 × 105N m–2 | |
| At the point B, pressure | = | Atmospheric pressure + pressure due to 80 cm = 0.8 m) height of liquid |
| = | P + hρg | |
| = | (1.013 × 105) + [0.8 × (0.9 × 103) × 9.8] | |
| = | (1.013 × 105) + (0.071 × 105) | |
| = | 1.084 × 105 N m–2 | |
| At the point C, pressure | = | Atmospheric pressure + pressure due to 120 cm = 1.2 m) height of liquid |
| = | (1.013 × 105) + [1.2 × (0.9 × 103) × 9.8] | |
| = | (1.013 × 105) + (0.1058 × 105) | |
| = | 1.119× 105N m–2 | |
| On making the tube vertical, at the point C, | ||
| pressure | = | Atmospheric pressure + pressure due to liquid column of height 220 cm (= 2.2 m) |
| = | (1.013 × 105) + [2.2 × (0.9 × 103) × 9.8] | |
| = | (1.013 × 105) + (0.1940 × 105) | |
| = | 1.207 × 105N m–2 |