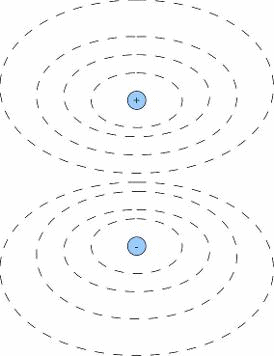
Equipotential surfaces due to a dipole
Equipotential surfaces can be shown as lines in two dimensions to provide a quantitative way of viewing electric potential.
Every point on a given line is at the same potential. Equipotential surfaces are the orthogonal trajectories (family of curves in the plane that intersect another family of curves at right angles) of electric field lines. Any electrostatic (conservative) field line penetrates such a surface normally (perpendicularly).
The electric field is always perpendicular to the equipotential surface which means that a charged particle moving along a equipotential surface always moves perpendicular to the electric force, therefore the electric force doesn't work on the particle moving along the equipotential surface.
The value of electrostatic potential at any two or more given points on such a surface is the same and is a constant. The work done by the field force in moving a charge along this surface is zero because there is no difference in potential between the initial and final points.
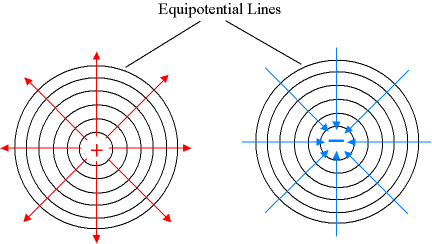Equipotential lines of two different positive charges and negative charges
Equipotential surfaces have to do with the change in electric potential. That is, as you go from one equipotential surface to another, the electric potential changes. When a charge moves from one equipotential surface to another either its kinetic energy increases (if the change is from a higher to a lower potential) or work must be done on it (if the change is from a lower to a higher potential). The electric force, like the gravitational force, is conservative. That is, if you do work on a charge to move it to a higher electric potential, this work can (in principle) be recovered in the form of kinetic energy as the charge "falls" back through this change in potential.
Properties of Equipotential Surfaces :
- Work done in moving a test charge over an equipotential surface is zero.
- Electric field is normal to the equipotential surface.
- These surfaces helps in distinguishing region of strong field from that of weak field.
- Equipotential surfaces gives the direction of electric field.
- These surfaces never cross each other.