Louis de Broglie (1892–1987)
French theoretical physicist, he took a doctorate at the Sorbonne and taught there, as the professor of
theoretical physics at the newly founded Henri Poincaire Institute (1928–1968). He established that all subatomic particles
can be described by either particle equations or by wave equations, thus laying the foundation of wave mechanics. In 1927, his
theory was proved experimentally with the measurement of the wavelength of the electron. This wave–particle duality was
used by Schrodinger in his formulation of quantum mechanics. In 1929, de Broglie received the Nobel prize for physics.
Light is a form of energy which sometimes behaves as waves and sometimes as particles (photons). Matter also can behave both like particles as well as waves. A wave is specified by the quantities like frequency , wavelength λ, amplitude and intensity. A particle is specified by its mass m, velocity v, momentum p and energy E. The concepts like interference, diffraction and polarization tell us that light is a wave. Experiments like photo–electric effect, Compton effect, black body radiations, X–ray spectra shows light in its particle nature. Louis de Broglie (1892–1987), a French physicist was the first to draw attention to this possibility. More specifically, he said that if a particle of mass m, moves with a velocity v then it behaves like a wave having a wavelength λ given by λ =h/(mv). He received a Nobel prize in 1928. Such a matter wave is sometimes referred to as de Broglie wave, and λ as the de Broglie wavelength. The wave associated with a moving particle is called matter wave or de Broglie wave and controls the particle in every respect. The intensity of a matter wave at a point represents the probability of the associated particle (e.g. electron) being there. Therefore, if the intensity of matter wave is large in a certain region, there is a greater probability of the particle being found there.
Electron diffraction pattern
Demonstration of wave–particle duality. An electron gun has been fired at a thin sheet of graphite.
The electrons passed through and hit a luminescent screen, producing the patterns of rings associated with diffraction.
Diffraction occurs when a wave passes through an aperture similar in size to its wavelength. But electrons are particles, so
should not exhibit the same phenomenon unless they can also behave like waves. De Broglie (1892–1987) correctly deduced
that this was the case and that particles have wavelengths inversely proportional to their momentum.
According to Planck's quantum theory, the energy of a photon of radiation of frequency and wavelength
λ is given by: E = h
............(i)
where h = Planck's constant,
If photon is considered as a particle of mass m, then according to Einstein's energy–mass relation, the energy E of the photon is given by: E = mc2 ..............(ii)
From equations (i) and (ii) we have, h
= mc2
The quantity mc, is the momentum p of the photon having mass m and traveling with velocity c.
Eq. (iii) gives de Broglie wavelength for a photon. According to de Broglie eq. (iii) is applicable to both
the photons of radiation and other material particles. Thus, if a material particle has mass m and moves with a velocity v,
its momentum is p = mv. According to de Broglie, the wavelength λ of the wave associated with this moving particle is:
Eq.(iv) is de Broglie wave equation for a moving material particle. We know that,
then, 2Em = (mv)2
2Em = p2
p = v(2Em)
But λ = h/p
λ = h/v(2Em) .............................(v)
Quantum waves
Computer model showing the movement of many waves (wave paths, intersecting blue and purple lines). The
paths represent the motion of particles which are behaving like waves (wave–particle duality). Quantum theory states that
the waves associated with the moving particles can collide to produce one random quantum wave, made up of waves moving in all
directions. The particles travel from the top of the image downwards, stopping when they reach the pink line in the lower frame.
The waves were modeled by Professor Eric Heller, Harvard University, USA.
Suppose an electron at rest has been accelerated through a potential difference of V volts and gains a velocity v. If m and e are the mass and charge of electron respectively, then Work done on electron, E = eV
Substituting the values of h (= 6.62 × 10−34 J.S), e ( = 1.6 × 10−19 C) and m (= 9 × 10−31 kg), we get,
For example, de Broglie wavelength (λ) of an electron that has been accelerated through a potential difference of 100V from rest is given by:
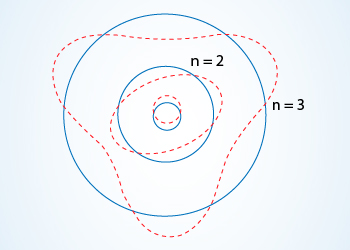The standing de Broglie waves set up in the first three Bohr orbits.
Matter waves are associated with material particles only if they are in motion. The de Broglie wavelength of a moving particle is independent of the charge and nature of the particle. The greater the momentum (mv) of the particle, the smaller is the wavelength of the wave associated with it and vice–versa. The matter waves travel faster as compared to electromagnetic waves. The velocity of matter waves is not constant since it depends upon the velocity of the material particle. However, velocity of electromagnetic wave is constant in a medium.