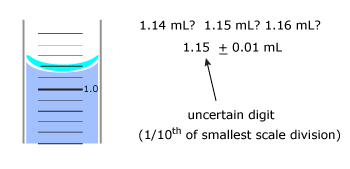
A quantity can never be measured exactly. Therefore, every measurement includes some uncertainty.
The acceptance of uncertainty depends upon the measuring device used. When we buy a piece of cloth, a scale that measures in 0.1cm increments is perfectly acceptable. It tells us that the length is, for example, 50 ± 0.1 cm. The term “± 0.1cm” expresses the uncertainty in the measurement: the length of the cloth between 49.9 and 50.1cm. The greater the number of digits in a measurement represents that the value has more certainty.
The uncertainty can be expressed with “±” sign, but generally we ignore the sign and assume an uncertainty of one unit in the right most digit. Both the certain and uncertain digits of a measurement are called significant figures. Finally, greater the number of significant figures in a measurement, greater is the certainty.

The number of significant figures can be defined as the number of digits necessary to express the results of a measurement consistent with the measured precision. The number of significant figures includes all the digits that are known and the first uncertain one.
The digit ‘zero’ is a significant figure under following conditions:
- If it is not the first digit of a number.
- If it is not used to place the decimal.
E.g: In 0.0257, the digit zero between decimal and 2 is used only to place the decimal and is not a significant figure. - If it falls between two other nonzero integer.
E.g: In 45,078, zero is a significant figure.
Worked Out Example
How many significant figure does each of the following numbers have?
(a) 4570
(b) 0.007
(c) 5000.0
(d) 0.04785
(e) 200.07
(f) 5.40 × 108
Solution:
| Number | Significant Figure | |
|---|---|---|
| (a) | 4570 | 4 |
| (b) | 0.007 | 1 |
| (c) | 5000.0 | 5 |
| (d) | 0.04785 | 4 |
| (e) | 200.07 | 5 |
| (f) | 5.40 × 108 | 3 |
Rounding off:
- If the digit following the last significant figure is greater than 5, the number is rounded to next higher digit.
E.g: 8.38 = 8.4 - If the digit following the last significant figure is less than 5, the number is rounded off to the present value of the
last significant figure.
E.g: 8.53 = 8.5 - If the last digit is 5, the number is rounded off to the nearest even digit.
E.g: 7.75 = 7.8
6.45 = 6.4
9.55 = 9.6