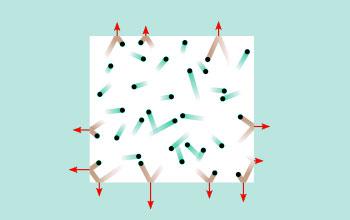
Pressure exerted by gas molecules due to collisions.
Collisions made by gas molecules on the walls of the
container are responsible for the pressure of the gas.
More the number of molecules more are the collisions,
leading to increase in pressure of the gas.
The kinetic theory of gases is developed with certain assumptions about the nature and state of motion of the molecules of gases. These assumptions are as follows:
- A gas consists of a very large number of extremely small molecules.
- The molecules are rigid and perfectly elastic spheres of very small diameters.
- All the molecules of a given gas are identical.
- Actual volume occupied by the molecules of a gas is very small compared to the volume occupied by the gas. There are lots of empty spaces.
- The intermolecular forces of attraction between gas molecules are negligible.
- The molecules are constantly moving in all possible directions, with different velocities in a random manner.
- In the course of their random motion, the molecules continuously collide with the walls of the container and with each other. These collisions give rise to the pressure exerted by the gas.
- The collisions are perfectly elastic. Hence, there is no loss of kinetic energy during the collisions.
- At a constant temperature, the average kinetic energy of the gas molecules remains constant. The average kinetic energy is directly proportional to the absolute temperature of the gas.
The pressure of gas is due to the collisions of the gas molecules with the walls of the container.
Postulates of kinetic molecular theory:
Kinetic molecular theory is based on following assumptions. They are:
- Particle volume: A gas consists of a large collection of individual particles. The volume of the individual particle is extremely small compared with the volume of the container. This model pictures gas particles as point of mass with empty space between them.
- Particle motion: Gas particles are in constant, random, straight line motion except when they collide with the container walls or with each other.
- Particle collisions: Collisions between the particles are elastic which means colliding molecules exchange energy but they do not lose any energy through friction. Thus their total kinetic energy (Ek) is constant. Between the collisions, the molecules do not influence each other by attractive or repulsive forces.
- Kinetic energy: The average kinetic energy of particle depends on the temperature of gas and nothing else.
Joseph Louis Gay–Lussac (1778 – 1850)
Joseph Louis Gay–Lussac (1778 – 1850)
was a French chemist and physicist. He formulated the law, Gay–Lussac's
law which states that if mass and volume of a gas are kept constant,
the pressure of gas increases linearly with increase in temperature.
He made a hot–air balloon with the help of Jean Biot to investigate
the differences in temperature and moisture in Earth's atmosphere by collecting
samples at different heights.
He was the discoverer of boron, also recognized iodine as a new element
and suggested the name ‘iode’.
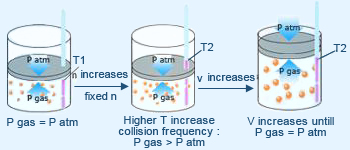Explanation of Charles's law by kinetic molecular theory.
Boyle's law states the inverse relationship between pressure and volume (P ∝ 1/V). The kinetic molecular theory agrees with this observation. Gay–Lussac's law finds a direct relationship between temperature and pressure (P ∝ T).
The kinetic molecular theory predicts an increase in gas pressure as temperature rises. Charles's law predicts a direct relationship between temperature and volume (V ∝ T). An increase in temperature increases both the force of each collision and the frequency of collisions as in Gay–Lussac's law.
Charles's law predicts a direct relationship between temperature and volume (V ∝ T). An increase in temperature increases both the force of each collision and the frequency of collisions as in Gay–Lussac's law.
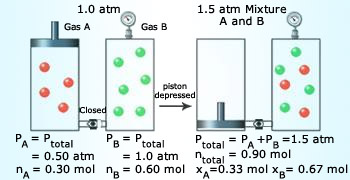Dalton's law of partial pressure.
Dalton's law of partial pressure
can be explained by the kinetic theory. With increase in
number of molecules, collisions increase, which in turn increase pressure.
Kinetic molecular theory agrees with the Dalton's law of partial pressure. Avogadro's law is also in agreement with the kinetic molecular theory. As a result, the volume expands until the number of collisions per unit of wall area is the same as it was before the addition.
The list of all postulates given above may be stated as the following equation:
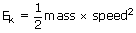
We have a relation between the average kinetic energy
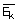and temperature which is a result of third postulate discussed earlier. The equation is given by,
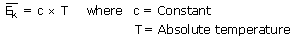
Using the primary definitions of velocity, momentum, force, and pressure a
derivation of this relationship given as,
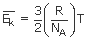
Where 'R' is the gas constant and 'NA' is Avogadro number.
From this it is evident that
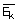is responsible for the gradations in temperature (be careful not to be confused
with total energy). Hence, as T increases,
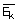increases.
From the general expression for kinetic energy of an object,
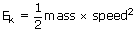
Apply it to the each molecule in a large population.
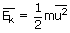
Where m is the molecular mass and u2 is the average of the
squares of the molecular speeds. On comparing the earlier obtained equation
of average kinetic energy with this we get,
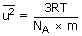
We know that NA.m is just molar mass 'M', on substituting and solving this we get
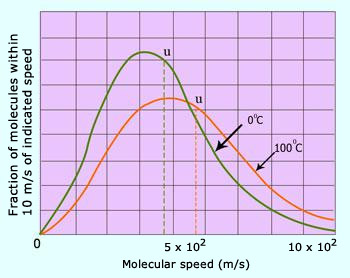Distribution of molecular speeds of N2 at 0°C and 100°C.
Root Mean Square velocity or R.M.S velocity (μrms).
A molecule moving at this speed has the average kinetic energy. Taking
the square root on both sides gives,
Where R is the gas constant, T is absolute temperature and M
is the molar mass.
Average (mean) velocity (A.V):
As denoted by the name it is the mean of the velocity of all the
molecules present within the gas. It is denoted by letter 'V'.
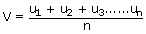
Where u1, u2, u3 are
the velocities of the gas molecules n is the number of molecules.
Relation between R.M.S velocity and A.V is given by the equation:
Average velocity (V) = 0.9213 × R.M.S velocity
Most probable velocity (M.P.V): The
velocity of the gas molecule keeps changing due to frequent collisions.
However, certain portions of gas molecules have same velocity. Velocity
possessed by a maximum number of gas molecules is termed as most probable
velocity. It is denoted by 'A'.
