Characteristics of Zero – Order reaction (Summary)
- Rate of reaction = r = k0 × [c]0
Units of rate of reaction = Conc. time− 1
= Mole.liter−1.sec− 1
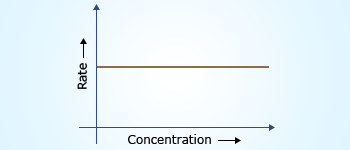
Rate doesn't depend on concentration.
- Rate equation:
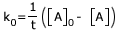
Units of rate constant = Conc. time− 1
= Mole.liter−1.sec− 1
Slope of the curve = rate constant 'k'.
- Half life:
.
So for a zero order reaction half life is directly proportional to the initial concentration.
Order is another term which is frequently used in chemical kinetics. Order of reaction is very significant in characterizing a type of reaction. The sum of powers of concentration terms in the rate equation is called total or over all order of the reaction.
For a reaction,
mA + nB 
Products
Rate = K[A]m[B]n
Total or overall order of reaction = m + n
Where, m = order with respect to A
n = Order with respect to B
Rates of reactions are specific pertaining to the order of the reactions. Every particular order will have its own rate. Depending on the order of the reactions there are different types of reactions:
- Zero Order reactions
- First Order reactions
- Second Order reactions
- Third Order reactions
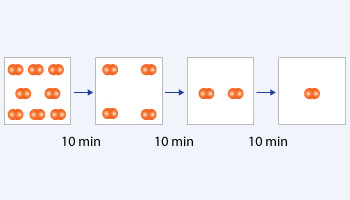First order reaction
In the above reaction initial concentration is 8 molecules. Time taking to consume 4 molecules is 10 minutes which is the half –life of the reaction. After first half –life the same time is taking to consume 2 molecules. After second half –life the same time is taking to consume 1 molecule. The half –life is independent of initial concentration hence it is a first order reaction.
Determination of order of reaction:
Integrated rate equations:
(1) By integration method: The experiments are carried out between the required amounts of reactants and products formed are analyzed in terms of values as desired in various integrated forms of order of reactions. Using experimental values, rate constant is obtained by using different order rate equations. The one which gives most constant value for rate constant suggests the order of reaction. This is also known as Hit and trial method. Most of the numerical problems are solved based on this method.
| Time | Reactant (Conc.) | Product (Conc.) | Rate constant (k) |
|---|---|---|---|
| t1 | (a − x1) | x1 | k1 |
| t2 | (a − x2) | x2 | k2 |
| t3 | (a − x3) | x3 | k3 |
| ∞ | 0 | x |
(2) Graphical method: Experiments are made to obtain the rates of reactions at different intervals using different amounts of reactants. Now the rates are plotted against (a−x)n values. The nature of graph suggests order of reaction. In first order reaction straight line is obtained when rate is plotted against (a−x). In zero order reaction a straight line parallel to X–axis is formed.
Second order reaction
In the above reaction initial concentration is 8 molecules time taking to consume 4 molecules is 5 minutes which is the half – life of the reaction. After first half – life 10 minutes is taken to consume 2 molecules. After second half – life 20 minutes is taken to consume 1 molecule. The half – life is inversely proportional to the initial concentration hence it is a second order reaction.
(3) Half life method: The relation between Half life (t1/2) and initial concentration (a) are given below
t ½ ∝ (a)1−n where n is the order of reaction
| Order of reaction | Half life | Unit of rate constant |
|---|---|---|
| 0 | t1/2 ∝ a | mol liter−1 time −1 |
| 1 | t1/2 ∝ (a)0 | time −1 |
| 2 | t1/2 ∝ (a)−1 | mol−1 liter1 time −1 |
| 3 | t1/2 ∝ (a)−2 | mol−2liter2 time−1 |
| n | t1/2 ∝ (a)1− n | mol1− n litern −1 time−1 |
(4) Ostwald's Isolation method: In this method a series of experiments are carried out. In each experiment, except one reactant the conc. of all other reactants are taken in excess and the order of reaction is determined. The reactant which is not taken in excess is said to be isolated and the obtained order of reaction becomes the order of reaction with respect to the isolated reactant.
(5) Vant – Hoff's differential method: It is based on rate expression of respective order of reaction. The rate at different concentration is measured and take the ratio of rate and concentrations to derive the order of reaction.
r ∝ c0 (zero) r ∝ c1 (1st) r ∝ c2 (2nd) r ∝ c3 (3rd) r ∝ cn (nth)
∴ r ∝ cn