Arrhenius acids dissociate to form aqueous H+ ions and Arrhenius bases dissociate to form aqueous
OH− ions.NOTE: The stronger the acid and base, the more dissociation will occur.
Arrhenius equation was first proposed by Dutch chemist J.H.van't Hoff in 1884. Five years later in 1889, the Swedish Chemist Svante Arrhenius provided a physical justification and interpretation for it. Currently, it is best seen as an empirical relationship.
He found that most reaction – rate data obeyed an equation based on three factors:
(a) The fraction of molecules possessing energy of activation are greater.
(b) The number of collisions occurring per second, and
(c) The fraction of collisions that have the appropriate orientation. These three factors are incorporated in
the Arrhenius Equation
Worked out example
The rate const. of a 2nd order reaction is 5.70 × 10− 5
dm3 mol− 1s− 1 at 25°C and 1.64 ×
10−4dm3 mol− 1 s− 1 at 40°C.
Calculate the activation energy.
Sol: Substituting the given data in Eq. we have,
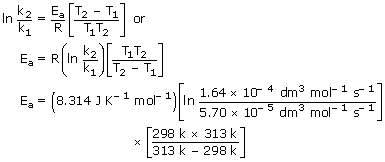
= 54478 J mol−1
= 54.48 kJ mol− 1
Arrhenius Equation
K = A e −Ea/ RT
K = rate constant Ea = activation energy R = gas constant (8.314 J / mol −k )
T = absolute temperature A = frequency factor.
A is related to the frequency of collisions and the probability that the collisions are favorably oriented for reaction. As the magnitude of Ea increases, k becomes smaller because the fraction of molecules that possess the required energy is smaller. Thus, reaction rates decrease as the energy barrier increases.
Taking the natural log on both sides of above equation, we have
ln K = − Ea / RT + ln A
The above equation has a form of a straight line. It predicts that a graph of ln k versus 1 / T will be a line with a slope equal to – Ea / R and a y –intercept equal to ln A.
Suppose that at two different temperatures, T1 and T2, a reaction has rate constants K1 and K2. ln ( k2 / k1) = Ea / R ( 1 / T1 − 1 / T2)
The above equation provides a convenient way to calculate the rate constant K1, at some temperature T1, when we know the activation energy and the rate constant K2, at some other temperature T2.