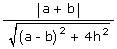If θ is an angle between the lines represented by ax² + 2hxy + by² = 0, then cos θ = ±

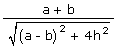
Let ax² + 2hxy + by² = 0 represent the two lines

l₁x + m₁y = 0 ----- (1)

l₂x + m₂y = 0 ----- (2)

∴ ax² + 2hxy + by² = 0 ≡ (l₁x + m₁y) (l₂x + m₂y)

Comparing both sides, we have

l₁l₂ = a;   l₁m₂ + l₂m₁ = 2h;   m₁m₂ = b

If θ is an angle between the lines (1) and (2), then

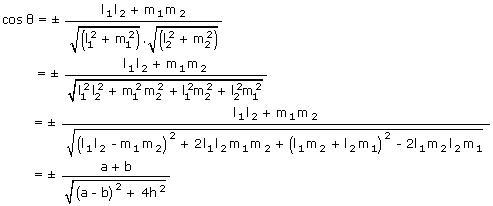
In particular,if θ is the acute angle between the lines represented by ax² + 2hxy + by² = 0, then cos θ =