Example
Ex 1:
Show that the lines joining the origin to the points of intersection of the curve x2 – xy + y2 + 3x + 3y – 2 = 0 and the straight line x – y – √2 = 0 are mutually perpendicular.
Sol:
Equation of the curve is x2 – xy + y2 + 3x + 3y – 2 = 0 ... (i)
Equation of the line is x – y – √2 = 0
x – y = √2
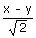 = 1 ... (ii)
= 1 ... (ii)Homogenising, (i) with the help of (ii)
x2 – xy + y2 + 3x.1 + 3y.1 – 2.12 = 0
x2 – xy + y2 + 3(x + y) 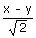 – 2
– 2 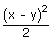 = 0
= 0
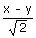 – 2
– 2 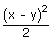 = 0
= 0x2 – xy + y2 + (3/√2) (x2 – y2)
– (x2 – 2xy + y2) = 0
x2 – xy + y2 + (3/√2) x2 – (3/√2)
y2 – x2 + 2xy – y2 = 0
(3/√2) x2 + xy – (3/√2) y2 = 0
Comparing with ax2 + 2hxy + by2 = 0
a = (3/√2), b = –(3/√2) and h = 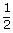
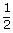
⇒ a + b = (3/√2) – (3/√2) = 0
∴ The given lines are mutually perpendicular.