Examples

Ex 1:

(a) Simplify 5 × 5³.

Sol:

5 × 5³ = ?

The product law: a^m × aⁿ = a^{m +
n}

a = 5, m = 1 and n = 3

5 × 5³	=	5¹ × 5³
	=	5^{1 + 3}
	=	5⁴
	=	5 × 5 × 5 × 5
	=	625

(b) Simplify (a^{– 4}b²) × (a²b²).

Sol:

We group the exponents with base 'a' and those with base 'b'

and apply the same formula as above.

(a^{– 4}b²) × (a²b²) = (a^{– 4}a²) × (b²b²)

The product law: a^m × aⁿ = a^{m + n}

Here in the first group at RHS: a = a, m = – 4 and n = 2
while in the second group: a = b, m = 2 and n = 2

(a^{– 4}b²) × (a²b²)	=	(a^{– 4}a²) × (b²b²)
	=	(a^{– 4 + 2}) × (b^{2 + 2})
	=	a^{– 2}b⁴

Ex 2:

Simplify 5(y⁹ ÷ y⁵).

Sol:

5(y⁹ ÷ y⁵) =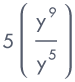

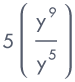
The quotient law:

Here a = y, m = 9 and n = 5

5(y⁹ ÷ y⁵)	=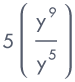
	=	5(y^{9 – 5})
	=	5y⁴

Ex 3:

Simplify (y²)⁶.

Sol:

(y²)⁶ = ?

The power of a power law: (a^m)ⁿ = a^{(m × n)}

Here a = y, m = 2 and n = 6

(y²)⁶	=	y^{2 × 6}
	=	y¹²

Ex 4:

Simplify (2 × 3)⁴.

Sol:

(2 × 3)⁴ = ?

The power of a product law: (ab)^m = a^m × b^m

Here a = 2, b = 3 and m = 4

(2 × 3)⁴	=	(2)⁴ × (3)⁴
	=	(2 × 2 × 2 × 2) (3 × 3 × 3 × 3)
	=	16 × 81
	=	1296

Ex 5:

Simplify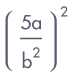

.

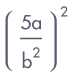Sol:

= ?

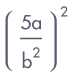The power of a quotient law:

Here a = 5a, b = b² and m = 2

Ex 6:

Simplify (3m⁸n³)¹ ÷ (3m⁸n³)⁰.

Sol:

(3m⁸n³)¹ ÷ (3m⁸n³)⁰ = ?

The zero exponent law: a⁰ = 1, a ≠ 0

Here a = 3m⁸n³ and noting a¹ = a

(3m⁸n³)¹ ÷ (3m⁸n³)⁰	=	3m⁸n³ ÷ 1
	=	3m⁸n³

Ex 7:

Find the value of 'x' in 3 × 5^x = 3/125.

Sol:

3 × 5^x = 3/125 = ?

The negative exponent law:

Ex 8:

Simplify (3a)^{–
2}.

Sol:

(3a)^{– 2} = ?

The negative exponent law:

Here a = 3a and n = 2

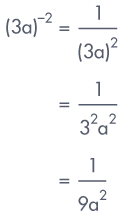
Ex 9:

Solve (– 9)³ ÷ (– 9)¹.

Sol:

Ex 10:

.

Sol:

We have

Ex 11:

Evaluate

.

Sol:

We have

Ex 12:

Evaluate

.

Sol:

We have

Ex 13:

Simplifies

.

Sol:

We have

Ex 14:

Find the value of x.

Sol:

Ex 15:

Find the value of

Sol: