Important points to remember

(i) The lines represented by ax² + 2hxy + by² = 0 and

ax² + 2hxy + by² + 2gx + 2fy + c = 0 form:

(a) a parallelogram if a + b ≠ 0, (a – b)fg + h (f ² – g²) ≠ 0

(b) a rectangle if a + b = 0, (a – b)fg + h (f ² – g²) ≠ 0

(d) a square if (a + b) = 0, (a – b)fg + h (f ² – g²) = 0

(ii) The area of parallelogram formed by the two pairs of lines ax² + 2hxy + by² = 0 and ax² + 2hxy + by² + 2gx + 2fy + c = 0 is given by

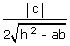
(iii) The product of the perpendicular distances from the origin to the pair of straight lines ax² + 2hxy + by² + 2gx + 2fy + c = 0 is given by

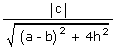
(iv) Length of the X-intercept made by the pair of lines ax² + 2hxy + by² + 2gx + 2fy + c = 0 is given by

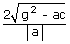
(v) Length of the Y-intercept made by the pair of lines ax² + 2hxy + by² + 2gx + 2fy + c = 0 is given by

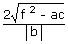
(vi) The product of the length of perpendiculars form (x₁, y₁) upon the lines ax² + 2hxy + by² + 2gx + 2fy + c = 0 is given by

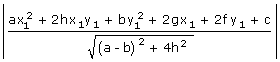
(vii) The condition that the pair of lines represented by

ax² + 2hxy + by² + 2gx + 2fy + c = 0 intersect on X-axis is g² = ac

(viii) The condition that the pair of lines represented by

ax² + 2hxy + by² + 2gx + 2fy + c = 0 intersect on Y-axis is f ² = bc

(ix) If ax² + 2hxy + by² = 0 are two sides of a parallelogram and lx + my = 1 is one diagonal, then the equation to the other diagonal is

y(bl – hm) = x(am – hl)

(x) If (kl, km) is the orthocenter of the triangle formed by the lines ax² + 2hxy + by² = 0 and lx + my = 1, then

k =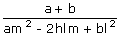

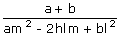
(xi) If ax² + 2hxy + by² = 0 represents two sides of a triangle for which (c, d) is the orthocenter, then the equation of the third side is

(a + b) (cx + dy) = ad² – 2hcd + bc²

(xii) The condition that the slopes of the lines represented by ax² + 2hxy + by² = 0

are in the ratio p : q is ab given by

(p + q)² = 4h²pq